"Did you try to play at 80cm on Etherwave?" - Buggins
No, but one with the ESPE01 or YAEWSBM might be somewhat playable there, but even then the "playing" would most likely only be suited to effects and such.
"So, I completely disagree with part 1 of your calculations."
I see what you are saying, and I don't entirely disagree with you disagreeing with me! ![]()
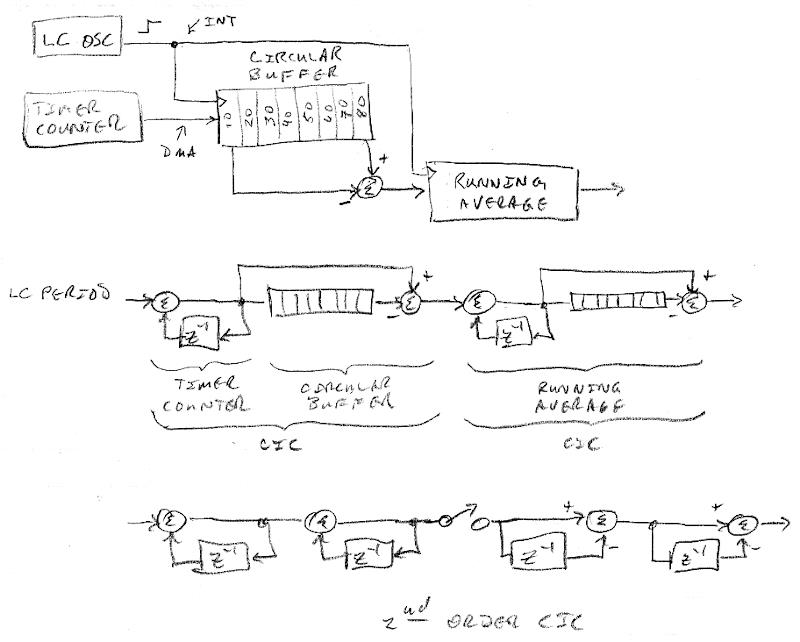
What's at the heart of this is how the "noise" is characterized. For theoretical calculations it is usually treated as zero mean white noise, but here the "noise" is clearly correlated between samples. Whatever error a single period measurement has is made up for in the next, so after many consecutive period measurements the error or uncertainty or noise is still one sample clock period.
Let me use the previous analogy because it better reflects the final implementation (a Theremin axis) and I'm simplifying the numbers a bit:
- LC resonance is 1MHz, we sample this at 100MHz and then sub-sample that at 1kHz.
- Sampling error is correlated so the 1kHz sub-sample will only have one clock of 100MHz of "nose" or error.
- 100MHz / 1kHz = 100,000 = ~17 bits.
So I was wrong by a wide margin here because I was treating the noise as uncorrelated.
However, if there are only 4 bits of "changing" information out of a total of 8, then I believe we would have to reduce this to 17 - 4 = 11 13 bits of "real" postional information. I mean, the 17 bits above have a limited dynamic range of 4 bits out of 8 bits. Does that make sense?
Because the noise is correlated, I don't believe further inspection and comparisons of the data with different shifts will yield much in the way of further benefit (i.e. higher order CIC or similar). Some perhaps, but not as much because there isn't as much uncorrelated noise to filter away. I mean, if you shift the circular buffer by one, pulling in one new sample and throwing away one older sample, the average isn't going to change much if you average this with the previous average. You'll get a smoother output, but I don't think it will net you as much in terms of resolution increase as the uncorrelated case can.
Actually, by shifting and overlapping the measurements by 1mm, as in your second example, I believe you are introducing uncorrelated noise for each, and I'm not sure if that might actually help or hurt the final average. There are real scenarios where more measurement actually hurts the SNR.
Of course you can take the output and filter it again down to 100Hz and increase the resolution ~1.6 bits. Or you could immediately go from 100MHz to 100Hz and gain ~3.3 bits due to the correlation. But then you might hear zippering if you don't do further filtering.
[EDIT] Vadim, I hope you don't think I'm arguing with you, or disagreeing just to be disagreeable, you are really helping me to straighten out my own thoughts regarding sampling. I appreciate it when you point out the flaws in my reasoning. As Feynman said, the objective is to prove yourself wrong as fast as possible! I'm also not playing "devils' advocate" here, I want to understand this as well as you do. I don't get a lot of opportunity to bounce this stuff off of people who are also in the process of thinking it through.
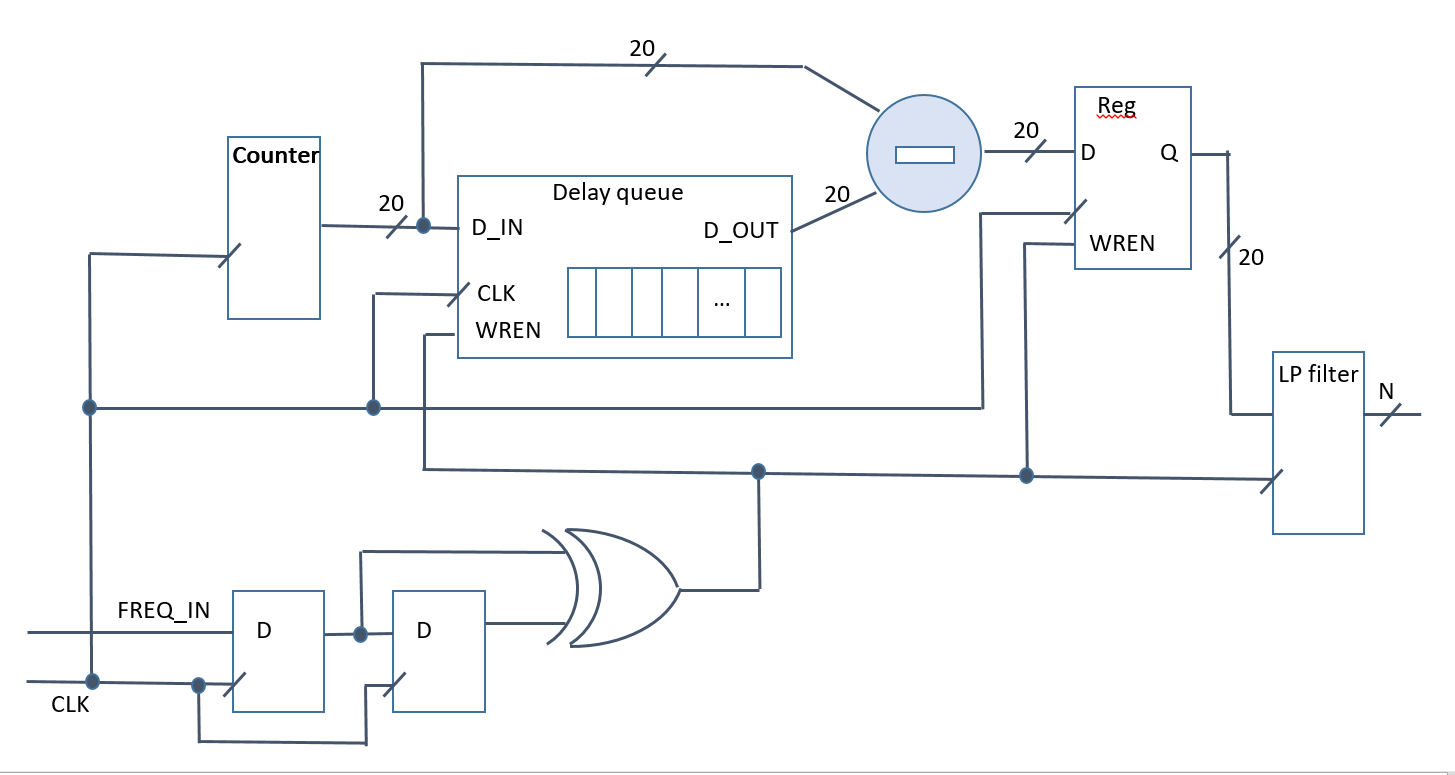
[EDIT2] The real trick would be to somehow keep the noise correlated through the entire process, but I think uncorrelated noise is ultimately introduced whenever the value is actually measured to be used. I mean, every time you discard samples from the average you are starting it at a new location, which introduces new uncertainty or noise. But if the sample discard is total after a single use, then the new start point is the old end point, and that would seem to minimize uncertainty. I suppose there is a reason integrate-and-dump is called a "matched filter".



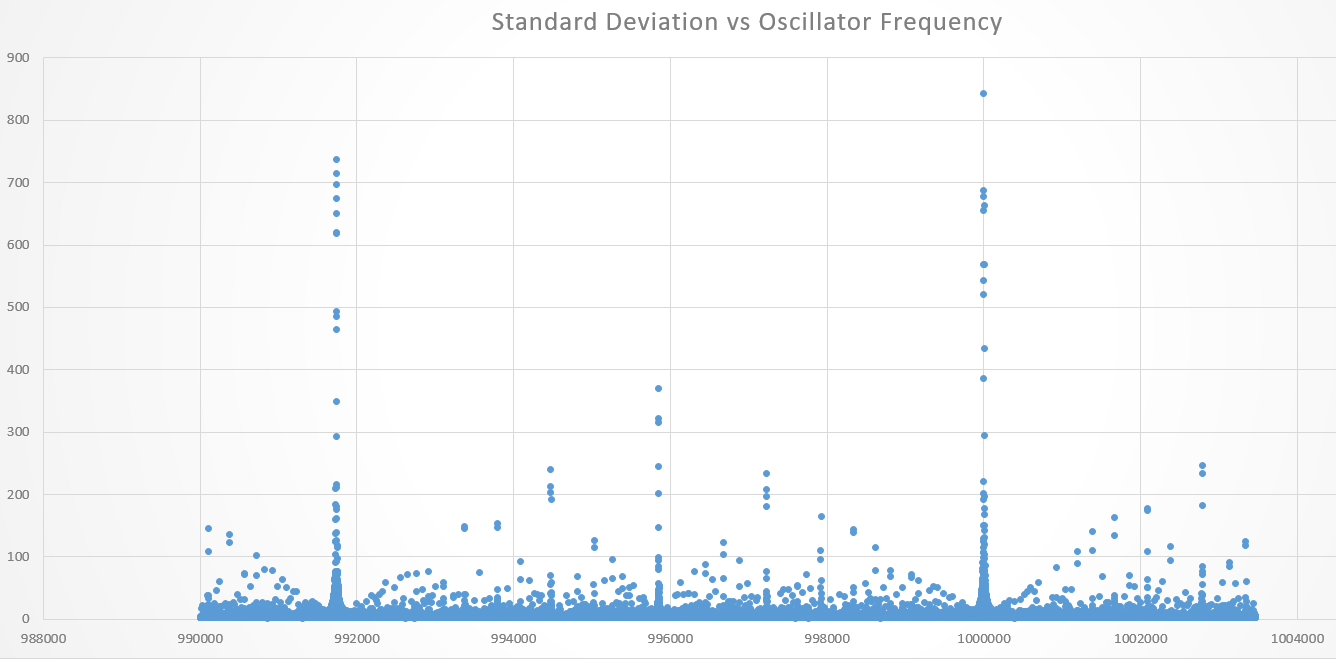 Filter output max-min value from exact value by frequency:
Filter output max-min value from exact value by frequency:
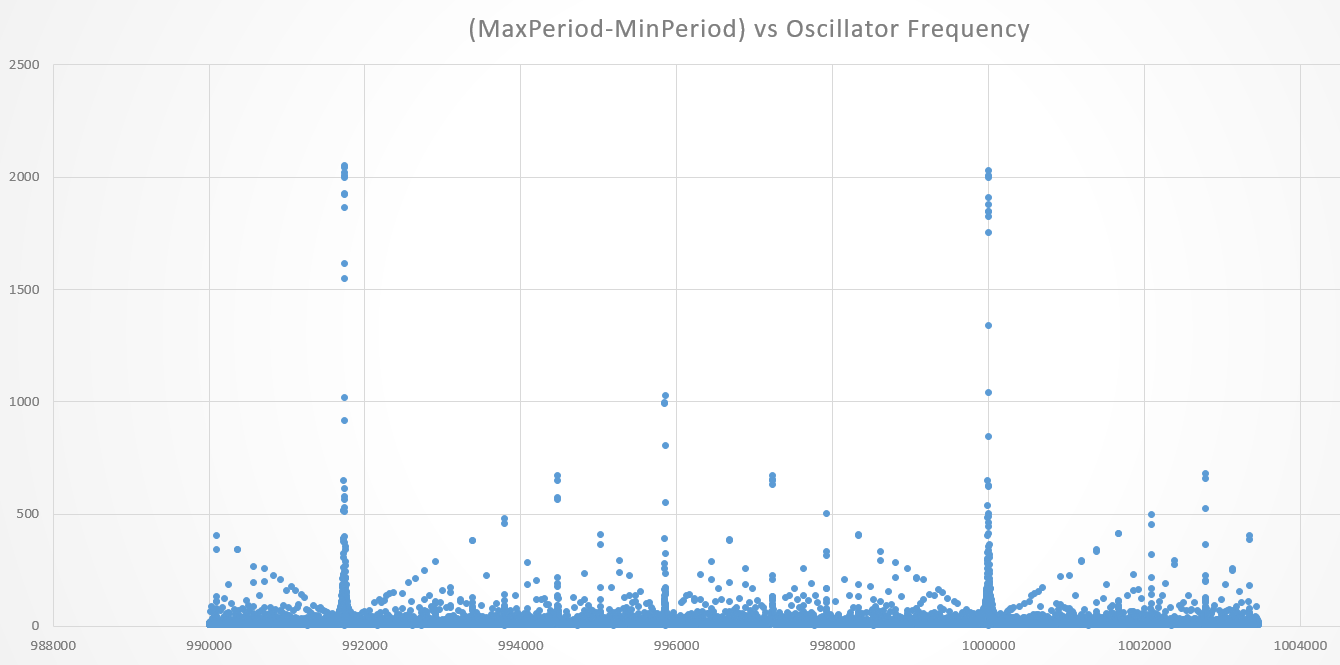 As you can see there are some cursed places where our filter performance reduces (twice in worst case - up to half of bits we gained by filtering (10 of 20) is getting rotten here.
As we can guess, these places are close to F_timer / integer divider. Or even rational F_timer * a / b.
[code]freq diff width period min max-min avg exactS
999983.981453462 2048 2048 503324539 31 503324544.10 8.150
999984.4302524126 2048 2048 503324299 88 503324322.50 33.497
999984.8790513631 2048 2048 503324045 151 503324079.00 45.238
999985.3278503136 2048 2048 503323776 212 503323877.53 74.600
999985.7766492642 2048 2048 503323506 275 503323652.97 89.426
999986.2254482147 2048 2048 503323322 231 503323393.43 79.685
999986.6742471652 2048 2048 503323139 169 503323172.80 50.634
999987.1230461157 2048 2048 503322942 95 503322952.97 25.174
999987.5718450663 2048 2048 503322732 29 503322736.83 8.050
999988.0206440168 2048 2048 503322506 36 503322509.77 7.479
999988.4694429673 2048 2048 503322262 121 503322283.57 34.778
999988.9182419179 2048 2048 503321998 188 503322049.10 65.659
999989.3670408684 2048 2048 503321713 299 503321847.97 104.870
999989.8158398189 2048 2048 503321404 402 503321573.27 128.649
999990.2646387694 2048 2048 503321246 324 503321351.17 114.292
999990.71343772 2048 2048 503321082 253 503321162.43 83.732
999991.1622366705 2048 2048 503320899 153 503320943.73 56.638
999991.611035621 2048 2048 503320698 41 503320701.13 8.894
999992.0598345716 2048 2048 503320472 46 503320476.23 8.696
999992.5086335221 2048 2048 503320220 159 503320250.80 50.167
999992.9574324726 2048 2048 503319938 289 503320034.07 106.266
999993.4062314231 2048 2048 503319616 479 503319800.83 148.597
999993.8550303737 2048 2048 503319248 645 503319626.77 199.868
999994.3038293242 2048 2048 503319111 534 503319325.80 190.233
999994.7526282747 2048 2048 503318986 440 503319076.33 122.653
999995.2014272253 2048 2048 503318838 266 503318887.93 89.076
999995.6502261758 2048 2048 503318659 112 503318666.37 22.832
999996.0990251263 2048 2048 503318438 65 503318441.73 11.530
999996.5478240768 2048 2048 503318161 334 503318209.63 98.271
999996.9966230274 2048 2048 503317799 618 503317951.03 219.672
999997.4454219779 2048 2048 503317313 1036 503317790.10 383.846
999997.8942209284 2048 2048 503316617 1819 503317432.53 541.696
999998.343019879 2048 2048 503316480 1750 503317089.87 676.028
999998.7918188295 2048 2048 503316480 2026 503317347.77 840.596
999999.24061778 2048 2048 503316480 1872 503316809.43 566.992
999999.6894167305 2048 2048 503316480 1843 503316667.30 519.839
1000000.1382156811 2048 2048 503316480 0 503316480.00 69.566
1000000.5870146316 2048 2048 503314577 1903 503316018.33 685.760
1000001.0358135821 2048 2048 503314637 1843 503315956.07 653.456
1000001.4846125327 2048 2048 503314479 2001 503315897.33 662.450
1000001.9334114832 2048 2048 503314486 1994 503315660.87 566.431
1000002.3822104337 2048 2048 503314546 1337 503315404.70 433.153
1000002.8310093842 2048 2048 503314489 840 503315070.00 293.040
1000003.2798083348 2048 2048 503314469 457 503314844.70 149.344
1000003.7286072853 2048 2048 503314531 90 503314611.97 20.766
1000004.1774062358 2048 2048 503314377 3 503314378.80 1.585
1000004.6262051864 2048 2048 503313954 232 503314156.27 73.217
1000005.0750041369 2048 2048 503313620 407 503313886.77 141.448
1000005.5238030874 2048 2048 503313393 500 503313711.40 195.128
1000005.972602038 2048 2048 503313150 622 503313436.20 176.180
1000006.4214009885 2048 2048 503312997 483 503313275.73 165.963
1000006.870199939 2048 2048 503312789 351 503313014.50 118.524
1000007.3189988895 2048 2048 503312656 188 503312796.33 61.988
1000007.7677978401 2048 2048 503312483 98 503312570.47 23.391
1000008.2165967906 2048 2048 503312328 18 503312343.77 3.799
1000008.6653957411 2048 2048 503312012 124 503312120.53 34.179
1000009.1141946916 2048 2048 503311765 182 503311901.47 61.394
1000009.5629936422 2048 2048 503311472 301 503311635.90 102.436
1000010.0117925927 2048 2048 503311244 359 503311413.80 129.883
1000010.4605915432 2048 2048 503311046 316 503311203.97 96.245
1000010.9093904938 2048 2048 503310839 229 503310975.83 76.333
1000011.3581894443 2048 2048 503310657 140 503310772.47 40.703
1000011.8069883948 2048 2048 503310485 61 503310534.13 20.363
1000012.2557873453 2048 2048 503310311 2 503310311.67 0.711
1000012.7045862959 2048 2048 503310034 63 503310090.37 16.873
1000013.1533852464 2048 2048 503309765 131 503309860.67 44.940
1000013.6021841969 2048 2048 503309500 207 503309623.90 76.481
1000014.0509831475 2048 2048 503309261 270 503309397.53 82.326
1000014.499782098 2048 2048 503309049 243 503309196.23 85.265
1000014.9485810485 2048 2048 503308863 153 503308967.20 50.174
1000015.397379999 2048 2048 503308661 97 503308737.57 31.339
1000015.8461789496 2048 2048 503308455 57 503308499.47 17.702
1000016.2949779001 2048 2048 503308277 3 503308278.27 0.918
1000016.7437768506 2048 2048 503308015 45 503308054.00 12.276
1000017.1925758012 2048 2048 503307752 100 503307824.10 35.067
1000017.6413747517 2048 2048 503307503 152 503307590.60 54.935
1000018.0901737022 2048 2048 503307273 195 503307386.27 60.831
1000018.5389726528 2048 2048 503307047 192 503307138.57 68.618
1000018.9877716033 2048 2048 503306830 144 503306942.47 46.915
1000019.4365705538 2048 2048 503306624 96 503306699.20 29.672
1000019.8853695043 2048 2048 503306437 42 503306471.00 12.371
1000020.3341684549 2048 2048 503306243 5 503306245.63 1.198
1000020.7829674054 2048 2048 503305987 40 503306021.03 9.497
1000021.2317663559 2048 2048 503305732 82 503305804.67 22.830
1000021.6805653065 2048 2048 503305501 111 503305569.50 36.547
1000022.129364257 2048 2048 503305251 164 503305337.87 52.498
1000022.5781632075 2048 2048 503305027 165 503305109.83 53.537
1000023.026962158 2048 2048 503304810 125 503304897.83 41.569
1000023.4757611086 2048 2048 503304607 77 503304668.40 24.256
1000023.9245600591 2048 2048 503304401 44 503304439.87 9.214
As you can see there are some cursed places where our filter performance reduces (twice in worst case - up to half of bits we gained by filtering (10 of 20) is getting rotten here.
As we can guess, these places are close to F_timer / integer divider. Or even rational F_timer * a / b.
[code]freq diff width period min max-min avg exactS
999983.981453462 2048 2048 503324539 31 503324544.10 8.150
999984.4302524126 2048 2048 503324299 88 503324322.50 33.497
999984.8790513631 2048 2048 503324045 151 503324079.00 45.238
999985.3278503136 2048 2048 503323776 212 503323877.53 74.600
999985.7766492642 2048 2048 503323506 275 503323652.97 89.426
999986.2254482147 2048 2048 503323322 231 503323393.43 79.685
999986.6742471652 2048 2048 503323139 169 503323172.80 50.634
999987.1230461157 2048 2048 503322942 95 503322952.97 25.174
999987.5718450663 2048 2048 503322732 29 503322736.83 8.050
999988.0206440168 2048 2048 503322506 36 503322509.77 7.479
999988.4694429673 2048 2048 503322262 121 503322283.57 34.778
999988.9182419179 2048 2048 503321998 188 503322049.10 65.659
999989.3670408684 2048 2048 503321713 299 503321847.97 104.870
999989.8158398189 2048 2048 503321404 402 503321573.27 128.649
999990.2646387694 2048 2048 503321246 324 503321351.17 114.292
999990.71343772 2048 2048 503321082 253 503321162.43 83.732
999991.1622366705 2048 2048 503320899 153 503320943.73 56.638
999991.611035621 2048 2048 503320698 41 503320701.13 8.894
999992.0598345716 2048 2048 503320472 46 503320476.23 8.696
999992.5086335221 2048 2048 503320220 159 503320250.80 50.167
999992.9574324726 2048 2048 503319938 289 503320034.07 106.266
999993.4062314231 2048 2048 503319616 479 503319800.83 148.597
999993.8550303737 2048 2048 503319248 645 503319626.77 199.868
999994.3038293242 2048 2048 503319111 534 503319325.80 190.233
999994.7526282747 2048 2048 503318986 440 503319076.33 122.653
999995.2014272253 2048 2048 503318838 266 503318887.93 89.076
999995.6502261758 2048 2048 503318659 112 503318666.37 22.832
999996.0990251263 2048 2048 503318438 65 503318441.73 11.530
999996.5478240768 2048 2048 503318161 334 503318209.63 98.271
999996.9966230274 2048 2048 503317799 618 503317951.03 219.672
999997.4454219779 2048 2048 503317313 1036 503317790.10 383.846
999997.8942209284 2048 2048 503316617 1819 503317432.53 541.696
999998.343019879 2048 2048 503316480 1750 503317089.87 676.028
999998.7918188295 2048 2048 503316480 2026 503317347.77 840.596
999999.24061778 2048 2048 503316480 1872 503316809.43 566.992
999999.6894167305 2048 2048 503316480 1843 503316667.30 519.839
1000000.1382156811 2048 2048 503316480 0 503316480.00 69.566
1000000.5870146316 2048 2048 503314577 1903 503316018.33 685.760
1000001.0358135821 2048 2048 503314637 1843 503315956.07 653.456
1000001.4846125327 2048 2048 503314479 2001 503315897.33 662.450
1000001.9334114832 2048 2048 503314486 1994 503315660.87 566.431
1000002.3822104337 2048 2048 503314546 1337 503315404.70 433.153
1000002.8310093842 2048 2048 503314489 840 503315070.00 293.040
1000003.2798083348 2048 2048 503314469 457 503314844.70 149.344
1000003.7286072853 2048 2048 503314531 90 503314611.97 20.766
1000004.1774062358 2048 2048 503314377 3 503314378.80 1.585
1000004.6262051864 2048 2048 503313954 232 503314156.27 73.217
1000005.0750041369 2048 2048 503313620 407 503313886.77 141.448
1000005.5238030874 2048 2048 503313393 500 503313711.40 195.128
1000005.972602038 2048 2048 503313150 622 503313436.20 176.180
1000006.4214009885 2048 2048 503312997 483 503313275.73 165.963
1000006.870199939 2048 2048 503312789 351 503313014.50 118.524
1000007.3189988895 2048 2048 503312656 188 503312796.33 61.988
1000007.7677978401 2048 2048 503312483 98 503312570.47 23.391
1000008.2165967906 2048 2048 503312328 18 503312343.77 3.799
1000008.6653957411 2048 2048 503312012 124 503312120.53 34.179
1000009.1141946916 2048 2048 503311765 182 503311901.47 61.394
1000009.5629936422 2048 2048 503311472 301 503311635.90 102.436
1000010.0117925927 2048 2048 503311244 359 503311413.80 129.883
1000010.4605915432 2048 2048 503311046 316 503311203.97 96.245
1000010.9093904938 2048 2048 503310839 229 503310975.83 76.333
1000011.3581894443 2048 2048 503310657 140 503310772.47 40.703
1000011.8069883948 2048 2048 503310485 61 503310534.13 20.363
1000012.2557873453 2048 2048 503310311 2 503310311.67 0.711
1000012.7045862959 2048 2048 503310034 63 503310090.37 16.873
1000013.1533852464 2048 2048 503309765 131 503309860.67 44.940
1000013.6021841969 2048 2048 503309500 207 503309623.90 76.481
1000014.0509831475 2048 2048 503309261 270 503309397.53 82.326
1000014.499782098 2048 2048 503309049 243 503309196.23 85.265
1000014.9485810485 2048 2048 503308863 153 503308967.20 50.174
1000015.397379999 2048 2048 503308661 97 503308737.57 31.339
1000015.8461789496 2048 2048 503308455 57 503308499.47 17.702
1000016.2949779001 2048 2048 503308277 3 503308278.27 0.918
1000016.7437768506 2048 2048 503308015 45 503308054.00 12.276
1000017.1925758012 2048 2048 503307752 100 503307824.10 35.067
1000017.6413747517 2048 2048 503307503 152 503307590.60 54.935
1000018.0901737022 2048 2048 503307273 195 503307386.27 60.831
1000018.5389726528 2048 2048 503307047 192 503307138.57 68.618
1000018.9877716033 2048 2048 503306830 144 503306942.47 46.915
1000019.4365705538 2048 2048 503306624 96 503306699.20 29.672
1000019.8853695043 2048 2048 503306437 42 503306471.00 12.371
1000020.3341684549 2048 2048 503306243 5 503306245.63 1.198
1000020.7829674054 2048 2048 503305987 40 503306021.03 9.497
1000021.2317663559 2048 2048 503305732 82 503305804.67 22.830
1000021.6805653065 2048 2048 503305501 111 503305569.50 36.547
1000022.129364257 2048 2048 503305251 164 503305337.87 52.498
1000022.5781632075 2048 2048 503305027 165 503305109.83 53.537
1000023.026962158 2048 2048 503304810 125 503304897.83 41.569
1000023.4757611086 2048 2048 503304607 77 503304668.40 24.256
1000023.9245600591 2048 2048 503304401 44 503304439.87 9.214