BLITs and BLEPs and DPWs (Oh My!)
Having delved into the various alias reduction methods I thought I'd summarize them. These are methods to generate the standard analog synth waveforms (triangle, sawtooth, square) with reduced aliasing. The main "trick" behind all three is in exploiting the extra information one has about the ideal waveform (as it exists in the continuous amplitude and time space, such as analog) and utilizing this to construct something that is close to the sampled and band limited (digital) representation. I haven't actually done any BLIT or BLEP in practice nor in simulation.
I encountered BLIT (Band Limited Impulse Train) and BLEP (Band Limited step function, not sure where the "EP" comes from) on various coding sites, but it seemed the coders were mostly blindly following instructions from papers and copying each other, so there was little insight to be gained from their resulting floating point code.
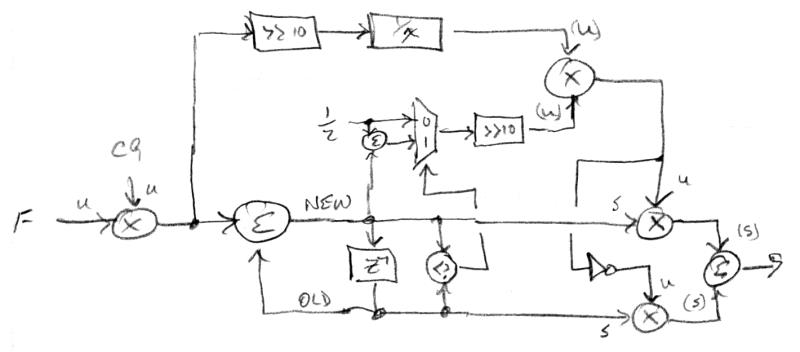
With BLIT they generate (via tables or polyphase FIR filter) a SYNC-like train of impulses (periodic spikes that have Gibbs Phenomenon "ringing" leading up to and trailing the spike). The impulses themselves are largely band-limited, so a string of positive ones can be "leaky" integrated to form ramps, but the leakage here must scale with frequency. An alternating string of positive and negative impulses can be simply integrated to form square waves (here minor constant leakage is used only to get rid of any DC bias).
With BLEP they concentrate on reducing the aliasing of instantaneous steps in the end waveform. The approach is very similar to BLIT (with tables or polyphase FIR filter) but they instead generate ringing, band-limited edges and merge these with the naively generated desired waveform. The polyphase filter approach can be quite efficient and effective at alias reduction.
Both BLIT and BLEP use the phase error information in the phase accumulator immediately after a modulo roll-over to fractionally position the output edge, which kills a good portion of the aliasing, and the Gibbs ripples lower it further. And if you think about it, this phase error isn't something you can trivially intuit after the fact. Running the naive (quantized) edge through a low pass filter will just average the positive and negative points, always returning a point that is roughly centered at zero, when what you need is a point that is more positive or negative based on the quantization error sign and magnitude. So THIS is why simple low pass filtering can't get rid of aliasing.
With DPW (Differentiated Parabolic Waveforms) they recognize that, over the cycle, a ramp is just a line with a slope. Mathematically integrating it gives x^2, or a parabola. If we then differentiate this (i.e. the phase ramp value squared) with a DSP filter type differentiator, a reduced alias ramp is produced, seemingly by magic! To better understand what's going on here I simulated it in Excel and compared the results of mathematical integration to DSP filter type integration. Again, the "trick" is that mathematical integration includes extra information about the phase that the filter type integration doesn't, and this info helps to fractionally position the sawtooth edge. A problem with this approach is that aliasing isn't eliminated, and this forces one to higher order mathematical integrations and more DSP differentiations. Which seems OK, but mathematical integration doesn't have the gain associated with an integration time constant, so one must scale the result 20dB (10x) per decade per order, which can really add up.
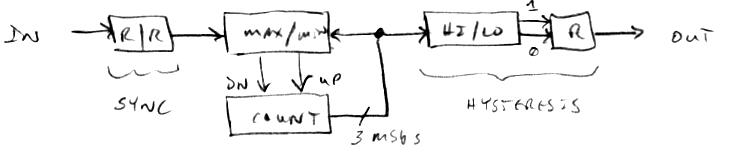
One of the simplest approaches is to comb filter (FIR or IIR) any aliasing in the gaps between the harmonics, and below the fundamental. The problems with this are that you have to know up-front if the waveform contains only odd or all harmonics, and the fractional delay filters employed are somewhat dispersive (non-harmonic) so they will interfere to some degree with the harmonics themselves. And the filter requires as much delay memory as the lowest fundamental you desire to put through it.
============
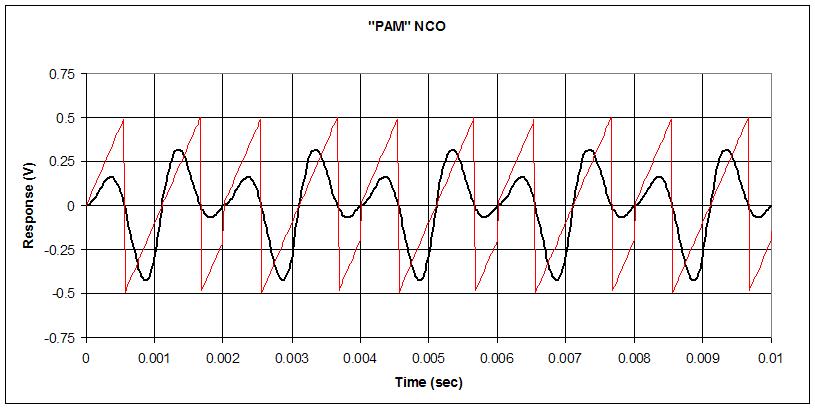
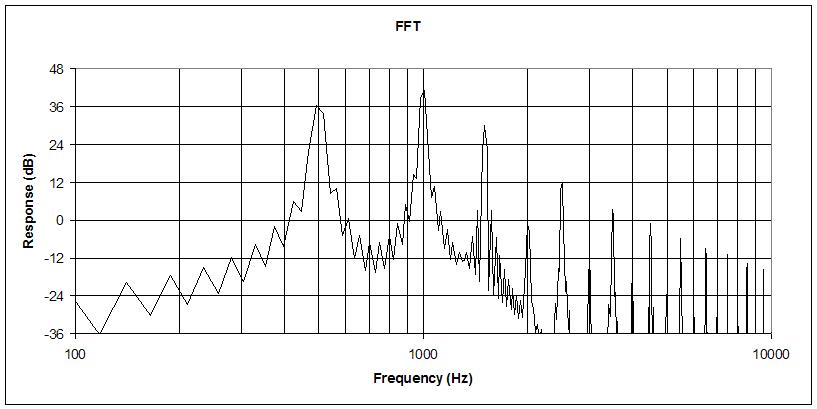
In the end, I'm pretty happy with my phase distortion-based oscillator. It gives me continuous and dynamic control over the slope of the harmonic roll-off, as well as all/odd/no harmonics, and doesn't alias too bad. And if I want screaming cats I can just use a tracking filter.
[EDIT] In a way, I think it's maybe a mistake to try to replicate what's going on in the analog synth world with 100% fidelity. If you want harmonics you can get them in many ways, and resulting waveforms don't have to even remotely look like the analog classics. I mean, those waveforms were picked mainly because they're relatively easy to generate with standard circuitry and such.
I must say, this exercise has got me thinking about harmonics in new ways. e.g. instead of clipping to get harmonics, maybe just run an amplitude-based control over the harmonic content input.