Q - The Winged Serpent
In the most general sense, Q (quality factor) is the ratio of energy stored vs. energy lost.
Inductors and capacitors store electrical energy. Some of this energy is converted via non-ideal parasitic mechanisms into other forms of energy (heat, RF, etc.) which then escape. Inductors and capacitors are AC devices, and when they are connected together in a closed circuit "tank", any stored energy will rather bizarrely alternately cycle from one to the other at a constant frequency (resonance). This cycling will gradually decrease in amplitude and eventually cease altogether (for all practical purposes) due to parasitic energy loss.
A good analogy here is a child on a swing: the swinging rate is fairly constant, and if energy isn't periodically added the amplitude will decrease to zero due to pivot friction, air resistance, etc. So one way to determine the Q here is to get the kid swinging, then stop pushing and examine the amplitude of two successive swings. The energy stored is proportional to the swing amplitude, so the energy lost is proportional to the difference in amplitude from one cycle to the next, and the Q is the ratio of these two quantities.
Continuing with the swing analogy, if we give the swing a properly timed push of constant energy each cycle, then the swinging will reach a certain constant amplitude - why? Because there are more friction and air resistances losses associated with a larger amplitude cycle, and at equilibrium our push is exactly making up for that loss. If we now try to abruptly stop the swinging child, we will probably get knocked over by the large amount of stored energy from all our pushing. The Q of the swinging child is equal to this stored energy divided by the energy of one push.
Similarly, if we examine a "ringing down" LC tank, the energy stored is proportional to the amplitude or voltage of the oscillations. So Q can be calculated by dividing the peak-to-peak voltage (Vpp) of one cycle by the difference in peak-to-peak voltage of the next cycle. If we do some fancy math, we find that the Q is equal to the the number of cycles it takes for the amplitude to reach 1/2 of the starting amplitude, multiplied by pi/ln(2) (~4.53).
And if we stimulate an LC tank by "pushing" it with a sine wave at the resonant frequency, the amplitude of the oscillations will reach a constant level which is directly dependent on the energy in the stimulus and the parasitic energy losses of the tank. Again, at equilibrium the energy of the stimulus equals the energy of the loss. The energy of both the stimulus and the energy stored in the tank is proportional to voltage, so the Q is the ratio of the tank oscillation amplitude voltage to the stimulus voltage oscillation amplitude voltage. So, for example, if the stimulus is 1Vpp and the tank amplitude is 100Vpp, then Q = 100Vpp / 1Vpp = 100.
Here is another way to view the LC tank: If we place the stimulus, inductor, and capacitor all in a loop, then the voltage across the capacitor will give us the second order low pass response of the stimulus. If the Q is high there will be a large peak in the response just as the low pass roll-off kicks in. If the stimulus (at resonance) is a square wave rather than sinusoidal, then the fundamental harmonic will be doing all the work, and the amplitude of this harmonic is 4/pi (~1.27) the peak-to-peak amplitude of the square wave. So if we wish to employ square waves to stimulate our LC tank, the tank voltage swing (at resonance) will be:
LC Vpp = square Vpp * Q * 4/pi
or about 27% higher than for sine stimulation. Working backwards to Q:
Q = LC Vpp / (square Vpp * 4/pi)
Square stimulation (at resonance) of a high Q LC low pass filter gives a fairly pure sine wave as output because the fundamental harmonic is strongly accentuated and the higher harmonics are strongly attenuated. This is desirable because square waves are easy to generate digitally.
============
If we're interested in measuring the Q of our Thremin coil and antenna, which method should we use? I think the ring-down method is probably the easiest, as it can be implemented with a scope and square wave generator running at some arbitrary low frequency, with the square wave used as scope trigger source, and the scope probe positioned somewhat near the antenna:
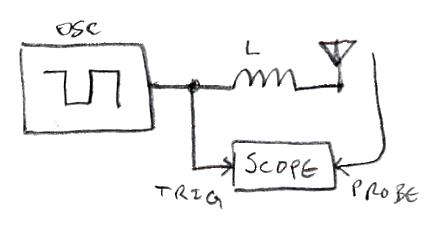
Not shown is the grounding here, make sure the generator and scope are earth grounded! And the coil and antenna should be positioned somewhat away from conducting objects.
Here is an example of what you might see on the scope:
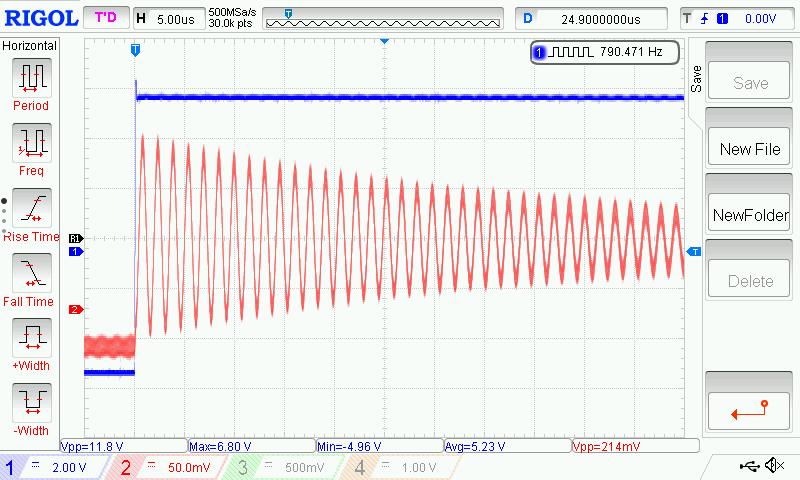
The blue trace is the low frequency square wave stimulus, the red trace is from the probe placed somewhat near the antenna. Counting the cycles to 1/2 amplitude, I see about 23. Q = 23 * 4.53 = 104. And this value of Q is very close to what I get when using the sine / square resonance stimulus voltage ratio method.
The impedance of the square wave generator should be somewhat lower than the DCR of the coil under test. You can lower the drive impedance by driving the coil through a resistive divider to ground (which will also lower the amplitude of the excitation step).
If you employ a capacitive divider in order to measure real voltages for these experiments, make sure it is at least a couple of feet away from the antenna and connected to it via rather thin wire, otherwise it will be bathed in the intense electrostatic field and likely give erroneous results.
[EDIT] And of course I left out what is probably the least intuitive way to measure Q, which also uses filter type concepts. Using the setup above, set the generator output for sine wave and increase the frequency until you hit LC resonance, which will give a huge peak-to-peak voltage on the scope. Note the frequency (f0) and amplitude (a0). Adjust the frequency down until the amplitude drops to a0 * 0.707 and note the frequency (f1). Adjust the frequency up past resonance until the amplitude drops to a0 * 0.707 and note the frequency (f2). (f2 - f1) is the absolute -3dB bandwidth, Q is the ratio of the resonance frequency to the bandwidth: Q = f0 / (f2 - f1).
[EDIT2] IMDb link: https://www.imdb.com/title/tt0084556/ (my least favorite of Larry Cohen's works).






