Let's Design and Build a (mostly) Digital Theremin!

I only ever implemented one crude reverb made up out of a couple delay lines, and IIRC, a few simple filters, but not sure anymore. Crude by what's available now anyway - I got the diagram from the 1980's "Musical Applications..." book by Hal Chamberlin, it was called a "good quality" stereo reverb It sounds somewhat metallic, but as long as it's only to make my synth experiments sound less dry without having to chain any other gear or software behind it, it has served me well enough.

"I got the diagram from the 1980's "Musical Applications..." book by Hal Chamberlin, it was called a "good quality" stereo reverb  It sounds somewhat metallic..."  - tinkeringdude

Yes, I played around somewhat with freeverb, which has similar topology, all of which almost certainly originated from the paper "Natural Sounding Artificial Reverberation" by M. R. Schroeder (1962!).  From what I recall, freeverb wasn't all that natural sounding.  William Grant Gardner's 1992 Master's thesis "The Virtual Acoustic Room" uses a cascade of all-pass and nested all-pass filters, with the output a mix of the intermediate nodes, and global feedback.  He states:

"Despite the attractiveness of these allpass structures for reverberator design, it is difficult to fashion a good sounding reverberator out of simple cascaded and nested allpasses. However, when some of the output of the allpass system is fed back to the input through a moderate delay, wonderful things happen. The harshness, buzziness, and metallic sound of the allpass system is smoothed out, possibly as a result of the increase in echo density caused by the outermost feedback path. This outermost feedback path is simply a comb filter. A lowpass filter can be inserted into this feedback path to simulate the lowpass effect of air absorption."

Running my Theremin stuff through my rudimentary speaker baffle sim (~notch comb filter, since removed) sometimes gave things a bit more complexity or character, sometimes not. Running the pretty nice (as digital pianos go, which are generally a crime against humanity) roland RD700NX SuperNatural Piano sound through the internal shitty reverb tends to cheapen it.  Go figure.

A fantastic book/paper on digital oscillators: http://argos.vu/wp-content/uploads/2016/05/Digital_Sound_Generation_1.pdf.  It includes most of the ones I looked into, as well as variations on the one I'm currently using.  Wish I'd found it earlier.

I'll say this: most synths don't have nearly enough filters to be really interesting.  Unless you're going for a "classic" (i.e. boring  IMO) analog synth sound, filtering is very often >90% of a realistic sounding timbre.  You need, absolute bare minimum, 6 formants, and the more the better, though there may be diminishing returns above 20 or so, and it may be possible to cover higher ranges (violins, cymbals, reverb) with formants + comb / all pass filters.

Constant Q -vs- Constant Decay Time

I can't find much on this issue with respect to synthesis, though Chamberlin touches on it in his book (in the "Percussive Sound Generation" chapter).  If you "ring" a constant high Q filter at various pitches, higher pitches will have shorter decay times (because the "rust" or damping removes energy per-cycle, and there are more cycles per second at higher frequencies). If you musically sweep a constant decay time filter over a large range then higher pitches will have higher Q.  Q is usually tied to peak gain, so if the Q isn't constant that would have to be explicitly dealt with, though dealing with it anyway is probably a good thing as it makes filter setting adjustments easier.  I imagine things like the human vocal resonant system and other natural systems are more or less constant Q due to the damping qualities of the physical construct?  I don't know.  "Classic" analog synth sound is constant Q, but is that what we generally want in a synth that's targeting physical systems? Angry wind sounds seem to be constant Q.

There is a possible middle ground here.  Both 2nd order bandpass integrators could be given damping feedback, one before the center frequency fractional multiplication, and one after, giving neither constant Q nor constant decay time with changing center frequency.  Though the construct might necessarily be inherently unstable at infinite Q.  (This is something I wasted a couple of hours proving to myself yesterday.  Chamberlin has a "Perfect" digital oscillator in the "Percussive Sound Generation" chapter which uses two delaying integrators in a loop, and his associated Basic code does the same.  If you simulate it with integers in Excel it quickly either dies or blows up.  Dattorro's excellent paper on "Effect Design" [LINK] discusses this and other topologies in depth.  If you use one delaying integrator and one non-delaying integrator in the loop it is amazingly and rather shockingly stable, though you don't get perfect quadrature at the sin and cos outputs due to the unequal integrator delays - though I believe you can fix this with a simple one clock averaging of the slow output and a one clock delay of the fast output.)

Noise Generation

Just starting to experiment with alternative filtering, and one great "diagnostic" signal to send through filters is white noise, to then be analyzed via FFT in Audition to directly display the frequency response. Which made me wonder how "white" my current generator was?  It was running a 32 bit LFSR for 8 cycles, then taking the 32 bits as a result, then inverting the sign bit. The FFT it looked pretty flat peak-wise, maybe a slight tilt down towards the DC end if you instead looked at the average.  Now, 8 LFSR cycles aren't the end of the world, but is there a faster way, so as to save a bit of real-time in the processor?

First, a couple of sanity check experiments.  I tried a single LFSR cycle with unsigned output - this gave a huge (~40dB down at 100Hz) spectral tilt towards DC, and you could easily hear the lack of low-end.  Next I tried a single LFSR cycle but converted the unsigned output to signed by flipping the most significant bit.  Wow, night and day! A bit of a hump, maybe 6dB, from 500Hz to 5kHz, though completely usable from a sonic standpoint.  Dattarro's paper that I pointed to above talks about all this (after you wade through the math and prose) and also shows a very simple EQ to improve it by subtracting 2x the previous output from the current output: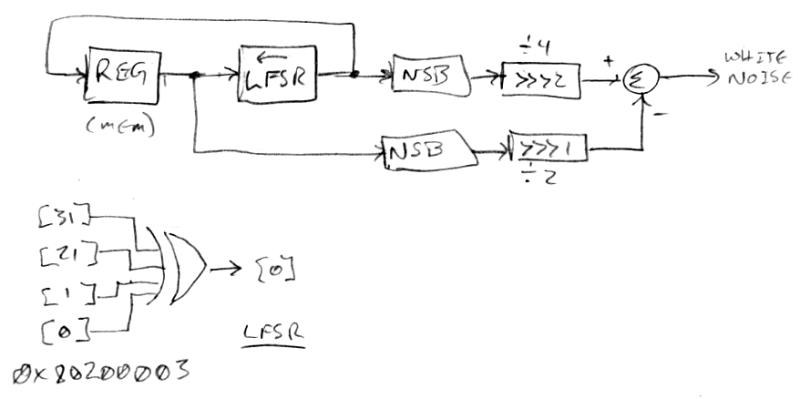

Above shows my current noise generator.  A memory location is read, an LFSR is performed on it (input is AND'ed with 0x80200003 and a bit reduction XOR performed on the result; output is the input shifted left by one; LSb of the output is the XOR result) and the result stored back in memory. Both the old and new LFSR unsigned results are converted to signed by flipping their sign bits, then scaled via signed shifts (I opted to scale down rather than up to provide headroom), then subtracted.  The FFT looks pretty damn flat (peak-wise) and it saves some real-time (down to just 15 cycles now).  I highly recommend this process!

[EDIT] There's a small but critical error in the above!  For a corrected version go here: [LINK]

Violin resonance again:

I just got a reply back from a former colleague, of whom I remembered that he had as his thesis making an expensive violin's sound out of a cheap toy violin via DSP. Keep in mind I don't understand a lot of those things and may make a translation error:
"Basically, there is a long FIR filter, for convolution with the impulse response of the [emulated] violin body. A bit of additional filtering, and all in all, quite a bit of computational power [dedicated DSP] to get convolution in the time domain with low latency."

Does kinda sound like it's too much going on for your spare cells or whatchamacallit in your FPGA, right?
Otherwise, the guy might look whether he can still find the paper, for some more details. (I'd have to translate them, though )

"Basically, there is a long FIR filter, for convolution with the impulse response of the [emulated] violin body. A bit of additional filtering, and all in all, quite a bit of computational power [dedicated DSP] to get convolution in the time domain with low latency."  - tinkeringdude

Thanks!  That's the right and most generic way to do this if you have the horsepower.

"Does kinda sound like it's too much going on for your spare cells or whatchamacallit in your FPGA, right?"

Yes, too much for my processor, though perhaps doable in FPGA fabric.  The main thing I don't like about the convolution approach is the huge amount of characterization data, which is a barrier to tweaking, fiddling (!) with, and altering the sound.  So I think I'm looking for a filtering add-on to the formant bank, but not formants per se.

Found an interesting site on the web where the author is using a Nord to do physical modeling synthesis of various instruments: http://electro-music.com/pm_tutorial/Index.htm

The violin & cello sounds he gets are quite realistic sounding, but the tutorial for these is unfortunately incomplete. There are a few pages that exist but that aren't linked to from the main page:

http://electro-music.com/pm_tutorial/Bow-Plucked.htm
http://electro-music.com/pm_tutorial/Bow-BowStringJunction.htm
http://electro-music.com/pm_tutorial/Bow-WoodenBody.htm
http://electro-music.com/pm_tutorial/Bow-Final.htm

The use of pulsed noise is interesting, and the body resonances are 48 explicit bandpass filters, which he says isn't sufficient, so he employs filter parameter morphing over a 3 semitone per entry spaced table.  Wish he'd finished that tutorial.

At one time Moog Inc. actually manufactured a "Moog CE String Filter" which someone provided external and internal pix of here: https://www.flickr.com/photos/macrutan/sets/72157629574187729/with/27333128556/.  Basically a box of 40 fixed frequency bandpass filters with variable global Q.  Here is someone who was reproducing the functionality of it at one point: https://web.archive.org/web/20080229000952/http://home.debitel.net/user/jhaible/jh_string_filter.html

People are discussing it here: https://forum.moogmusic.com/viewtopic.php?f=1&t=569&sid=5ea5cd4933002aa85bbf46f1e04f3c12 and someone in that thread reported: 

"I landed an ADA STD-1 tapped delay last year. That thing can get nice woody resonances. With the MIDImurf->STD-1 chain (using the Murf as a fixed filter bank) you can get scary good violins, violas, cellos, etc."

The MIDImurf is a lowpass filter and 7 bandpass filters with two selectable fixed 1.5 ratio tunings and variable global Q. The unfortunately named STD-1 is a now extinct multi-tapped analog delay line with feedback, which, when applied, forms a comb filter. Something very similar to this combo is the way I'm currently headed.

An interesting patent re. pulsed noise in string, woodwind, and vocal synthesis:
http://www.freepatentsonline.com/5157216.pdf.

There's a paper which is exceedingly similar: 
https://ccrma.stanford.edu/files/papers/stanm61.pdf

[EDIT] This seems to be (on paper) what I'm looking for, a nested multi-mode (including all, odd, and inharmonic) comb filter:
http://www.richarddudas.com/documents/ahn_dudas_icmc2013.pdf

With Bells On

Paper on mimicking a real bell via a highly dispersive comb filter with nested 2nd order all-pass in the feedback path (to make the poles non-harmonic) with sound samples (always fun):

http://legacy.spa.aalto.fi/demos/dafx02/

Probably easier (though probably less efficient real-time) to ring 7 bandpass filters, but it demonstrates what can be accomplished with delays and feedback.  I knew IIR combs were dispersive (which makes them a bit less useful as anti-aliasing filters) and was wondering if one could be made exaggeratedly so via all-pass feedback - the answer is clearly yes.

They use further constructs to create the low frequency beating, something a bandpass filter implementation would be naturally good at.

In conclusion: several bandpass formants for the low end and a dispersive comb or all-pass construct for the high end seems like it may be an efficient and useful general approach to a variety of complex resonant situations.

My Very Own SVF? (IGNORE THIS POST, SEE BELOW)

I believe I've come up with a novel State Variable Filter (SVF) form that solves some small but significant issues with the Chamberlin form: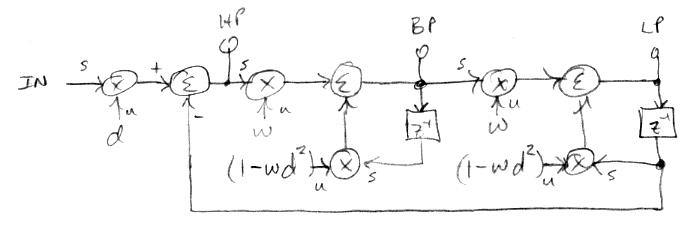

If so, I've got dibs on naming it the Wallin SVF!  It's basically a Chamberlin with damping at each integrator, rather than only at the first integrator.  One thing that's always bugged me about SVF damping is that critical damping is 1.414, or the square root of two.  If you don't care about integrator gain-up you can lump both frequency (w here) gains together as w^2, and this made me think an optimal damping situation might be damping both integrators separately, so that the damping value of 1 would be critical.  I haven't simulated this enough but I believe this might be the case.

Other changes are fairly superficial: the integrator positions have been swapped, and the damping attenuation is a loop gain reduction rather than full feedback with subtraction.  Previously I was juggling headroom (for low damping and low cutoff frequency gain-up) and footroom (for smooth decay).  But now that I'm explicitly reducing input gain to accommodate various damping settings, it makes more sense to left justify the input signal and do the center frequency gain reduction before the integrators as well.

The great Zolzer (who has his own SVF) wrote this great paper on filtering: http://www.music.mcgill.ca/~ich/classes/FiltersChap2.pdf

In it, he shows normalization of the SVF as input * sqrt(d) and filter feedback as d, as well as a low-pass "tilt" filter to equalize the high frequency end.  I don't believe my double damped SVF suffers from the high end issue, and bass response seems noticeably stronger and flatter now.  Zolzer also discusses various damping gain normalizations, and states:

"With a suitable normalization scheme the filter can prove to be very easy to handle whereas with the wrong normalization, the filter might be rejected by musicians because they cannot operate it."

Which I absolutely agree with.  Experimenting on the prototype, I found that normalizing for peak amplitude is surprisingly not the most musical, because the average sound level is more important to the ear.  So I squared the feedback damping term and this gives quite reasonable and even sounding loudness with damping change.  I'm also back to squaring the damping from the linear knob control value, so the input is actually normalized by damping squared, and the feedback is damping to the 4th power.  For a [0:63] control range, this conveniently gives human resonance values around midway (~32), strings around 24 or so, and much longer decays of bells and the like below 10, but with sufficient resolution on the low end.  Optimal normalization for narrow-band signals like sine waves and broadband signals like noise can be very different, but I think this provides a happy medium.

Anyway, here are a few quick string sounds with the (my?) new SVF: [LINK].  Still just 6 formants, but the bass response sounds more balanced.  I'll give this new SVF a good theoretical spreadsheet analysis shortly.  Then on to a comb / all-pass filter to provide even more resonances.

It's kind of weird turning up the Q (lowering the damping) of the formants when simulating a stringed instrument or a human voice.  Doing so gives acoustic room cues to my ears.

Double Damped SVF: not so good :-(

Finally simulating my double damped SVF and the results are not encouraging.  It makes an excellent lowpass filter, but bandpass and highpass don't look that good, with a low pass sort of shelving going on.  The various outputs sound more or less like you expect, particularly at lower damping / higher Q, but otherwise are kinda fugly at higher damping.  Damping of 1 does appear to give critical damping (maximally flat) for the low pass output.

Ah well, sorry to have jumped the gun on this, back to the Chamberlin form for me.

Especially the lowest sequence of notes sounds a lot like it's in an instrument body.
The attacks of the second and last sequence sound interesting. It does actually remind me of a sound I associated with the onset of friction on the string, with the bow, until it gets into steady motion. There is some slight movement in there. I wonder what does that. It's a very subtle thing though, so I'm not sure you'll know what I mean  (maybe it's even just in my head, heh)