EXP2 - Float
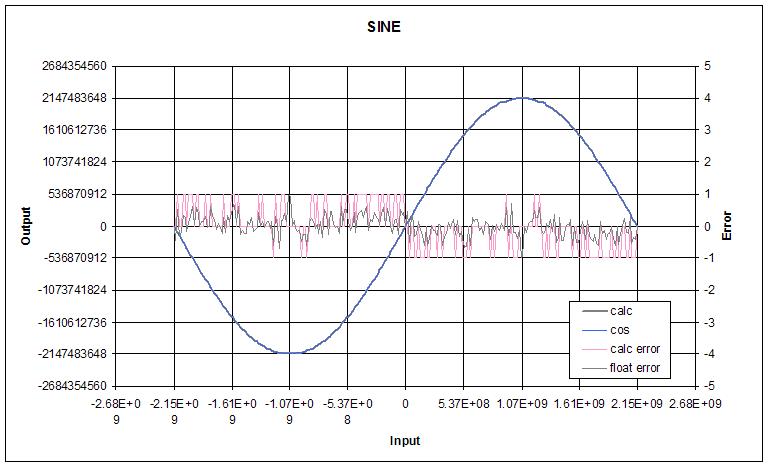
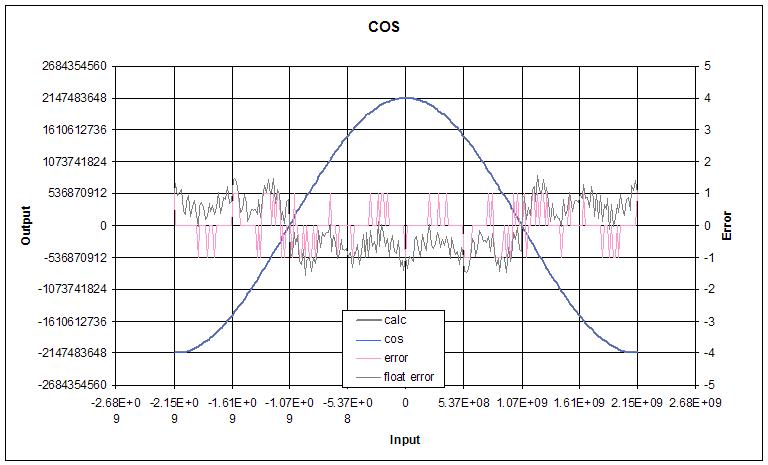
The motivation to develop a better EXP2 algorithm is mainly due to efficiency. The bit-by-bit square and multiply method I worked on before was accurate enough for Theremin use (provided one worked in a fudge factor) but very slow. Using polynomial approximation one can get essentially error-free results in a fraction of that time. And we need EXP2 in the first place because the plan is to calculate linear distance from capacitance, and the result of this must be exponentiated in order to conform with the ear's logarithmic response to pitch.
An exponential of the form 2^y where y is a non-negative integer may be implemented via a trivial left shifted one, with the shift distance given directly by the value of y. Evaluating a decimal exponential of the form 2^y.x is more involved. Because of a property of powers, a decimal exponential can be separated into an integer portion and a fractional portion:
2^y.x = 2^(y + 0.x) = (2^y) * (2^0.x) = (2^0.x) << y
So if we have a method to determine the fractional portion 2^0.x then all we need to do is shift this left by y in order to find 2^y.x.
The Taylor (actually Maclauren since the input is not offset) series polynomial for 2^x is:
2^x = 1 + (x^1 / 1!)(ln(2)) + (x^2 / 2!)(ln(2)^2) + (x^3 / 3!)(ln(2)^3) + (x^4 / 4!)(ln(2)^4) + ...
Since we desire adapting this to the full I/O range of 2^32 where we are only interested in the results of fractional inputs, we can scale and carefully adjust the coefficients to work optimally with a truncated series, and move the constant 1 to the other side of the equation, giving us:
2^x - 1 = Ax + Bx^2 + Cx^3 + Dx^4 + ...
This function is conveniently concave downward, which means there is no need to prescale the input or output to have the coefficients fit in the unsigned 32 bit space.
For a 32 bit process that employs a Hive type "extended unsigned" multiplies (i.e. the upper 32 bits of a 32 x 32 unsigned multiplication) the errors are as follows:
one x term: -370M
two x terms: +/-16M
three x terms: +/-650k
four x terms: +/-23k
five x terms: +/-600
six x terms: +/-80
seven x terms: +/-3
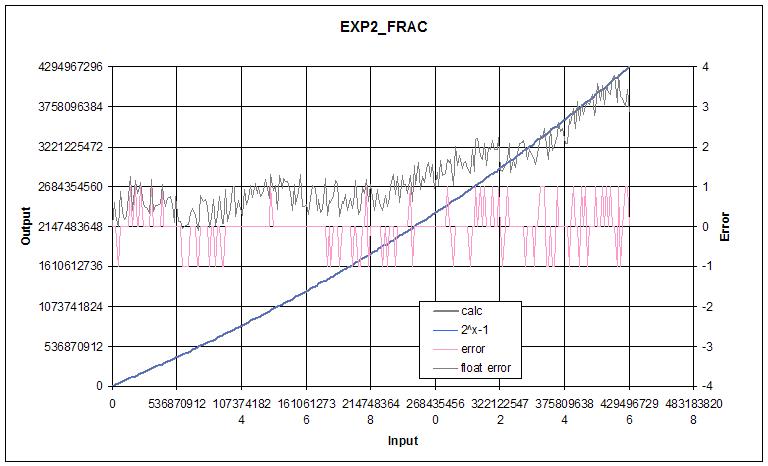
For 32 bit representations it seems worth going to 7 terms as the error at that point is negligible. It might be possible to reduce the error to +/-1 as there are only a few input values that give error larger than +/1, but I ran out of patience.
Mathematical operations are minimized by interleaving the power operations in with the coefficient operations:
poly = Ax + Bx^2 + Cx^3 + Dx^4 + Ex^5 + Fx^6 + Gx^7
poly = x(A + x[B + x(C + x[D + x(E + x[F + y(G)])])])
Because it is non-linear (unlike INV_F), EXP2 doesn't lend itself to linear scaling of input and output. In addition, EXP2 presents one with the very pressing need to implement some kind of decimal place indicator for both input and output - an EXPonent - which together with the input/output value - the SIGnificand - form floating point values. We require an input exponent because it tells us how to separate the input integer part from the fractional part for processing: the fractional part is evaluated via polynomial approximation and the input integer part forms the basis of the output exponent. And we strongly desire an output exponent because doing the actual shifting of the result would generally toss away many bits of precision. Implementing a float version of EXP2 is something of an algorithmic trial-by-fire, as it raises all sorts of thorny issues that must be dealt with.
The float convention that seems most natural to me is for the significand to have the decimal place to the left of the MSb. This gives an unsigned range of [0:1). One of the reasons it "seems most natural" is due to the fact that it is impossible for the multiplication of the significands to overflow with this arrangement, i.e. if both input values are guaranteed to be less than one then the multiplied result will always be less than one. This arrangement also maintains maximum precision for the truncated (i.e. chopped off LSb's) multiplied result. Since the unsigned representation has an implicit leading zero to the left of the decimal, the quantity 1 must be represented as 1/2 * 2^1, or SIG = 0b100...000 and EXP = 1.
There is a huge value in having floats fit into conventional spaces, and cleverly packed floats such as the IEEE754 - where the sign bit, biased exponent, and unsigned significand occupy a power of 2 bit width - may be conveniently arranged to undergo magnitude comparison as simple signed integers. But there are also major disadvantages. The packing and unpacking process is inefficient if it is not directly supported in hardware. Worse, whatever room is reserved for the exponent has an obvious and direct negative impact on the precision of the significand, so it is impossible to represent all signed n-bit integers with an n-bit float, forcing one to go to 2n floats if that is needed. Packed floats are a classic trade-off scenario.
The IEEE754 float specifies an implicit 1 to the left of the significand decimal point, yielding an unsigned range of [1:2) which clearly doubles the precision by adding a bit. But the downside is that significand multiplication overflow can occur, and underflow "denorms" - where the exponent low end limit is hit and the significand is allowed to take on values less than 1 - require special handling. I believe the implicit 1 is there mainly to make up somewhat for the loss of precision from packing, and not because it makes anything easier. With the given input range of [1:2), the output range of a multiply is [1:4), which complicates things.
IEEE854 generalizes IEEE754 and adds an "extended precision" type where the single precision significand occupies the full 32 bit space, and the exponent presumably some fraction of a second space. This seems geared towards processors that don't possess floating point hardware. It only places a lower bound on the width of the exponent, so I'm using 16 bits here because it's generally easier to use a power of 2 width.
Anyway, how do we handle the input and output exponents, and how do they influence the output significand? From the discussion above, we know how to generally handle the integer and fractional parts of the input. The fractional part is found via polynomial approximation, and the integer part simply shifts that left:
2^y.x = 2^(y + 0.x) = (2^y) * (2^0.x) = (2^0.x) << y
In terms of preprocessing, we have some input SIG_i and EXP_i that we have to translate into y (shift value) and 0.x (poly input value). In terms of post processing, we need to determine EXP_o, and massage the result of the polynomial approximation a little to determine SIG_o. Due to the float representation of the value 1 it won't be too surprising to discover a lot of +1 offsets in the EXP_o algorithm. Note that the poly result gives 2^(0.x) - 1, and not 2^(0.x), so a poly input of 0 gives a result of 0. We need to shift the poly result to the right once, add 0b1 (negate the MSb), and increment the exponent, which gives us the correct result of 2^0 = 1/2 * 2^1 = 1. We also need to keep in mind that Hive shifts are signed modulo and not internally limited in any way.
The most basic case to consider is when EXP_i is within the shift distance non-modulo limit [-32:31]. For the full range of EXP_i here, we set 0.x = SIG_i << EXP_i, which for non-negative EXP_i simultaneously left aligns the decimal portion 0.x with the implicit left decimal, and truncates away the upper integer portion y. Performing the opposite shift (i.e. EXP_i - 32) yields the upper integer portion y right aligned, which forms the basis of EXP_o: EXP_o = [SIG_i << (EXP_i - 32)] + 1. What about the case where EXP_i is within the modulo limits but negative? Here there is no integer portion y, so we set EXP_o = 1 and let the right shift of SIG_i naturally denormalize 0.x towards zero.
If (EXP_i < -32) then the input is to be right shifted beyond the basic data width of 32, to zero or past, so 0.x = 0. Since 2^0 = 1, we desire SIG_o = 0b100...000 and EXP_o = 1, which is satisfied by 0.x = 0 and EXP_o = 1. Since the (EXP_i < 0) case is already covered above, there is no new rule needed for it here.
If (EXP_i > 31) then the input is to be left shifted beyond the basic data width of 32, which means what exactly? Well, there can't be a fractional portion so 0.x = 0. And with no fractional portion we are dealing purely with integer powers of 2. In fact, EXP_o = [SIG_i << (EXP_i - 32)] + 1, just as in the basic case above. And this works until we hit overflow.
Underflow can't happen as very small inputs denorm to zero, giving 1 as the result. But overflow is definitely possible since we have an exponential input being exponentiated. How do we detect overflow? One way is to look at EXP_o and see if it exceeds the maximum. But we can't rely on this alone due to the modulo nature of the shifting - we won't get false positives from checking EXP_o but we can get false negatives. A method to see if we're close to overflow is to calculate how many bits EXP_o requires. Since EXP_o = [SIG_i << (EXP_i - 32)] + 1, we need to count the bits required by the SIG_i value, which can be found via 32 - lzc(SIG_i). Since this is shifted by EXP_i - 32 we can add the two to find the bits required: EXP_o bits = 32 - lzc(SIG_i) + EXP_i - 32, = EXP_i - lzc(SIG_i). It is unfortunate that the EXP_o calculation has the "+1" at the end because this creates a corner case, so we must also check the actual value of EXP_o itself.
Things not covered here are negative input (which should return an inverse result), rounding, overflow signaling, etc.
I've been wanting to do a deep dive on transcendental functions for what seems like forever, which I suppose is one of the reasons I'm dwelling so heavily on it now. I don't know why, but it's freakily satisfying seeing a polynomial with some input conditioning return essentially the same values as Excel over the full float range.